The Lagrangian hydrodynamics code

MAGMA2

Code paper: can be found *here*

In a nutshell:

• high-order Wendland kernels, each particle uses 300 neighbour particles for calculating densities and gradients
• accurate gradients via matrix-inversion techniques; the symmetries in the gradient expressions enable (like standard SPH-approaches) exact conservation
• "dissipation only where needed":
  • slope-limited reconstruction (similar to Finite Volume techniques)
  • entropy-based steering of dissipation parameters; details can be found *here*

Examples:

1. 3D Sedov-Taylor explosion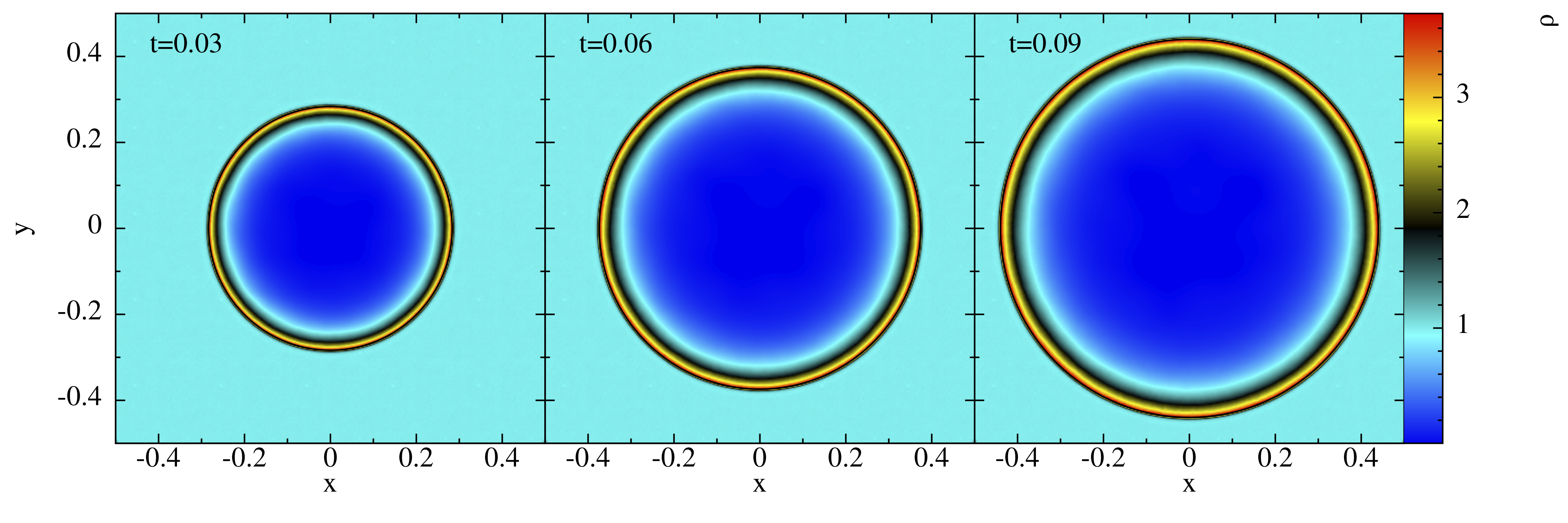





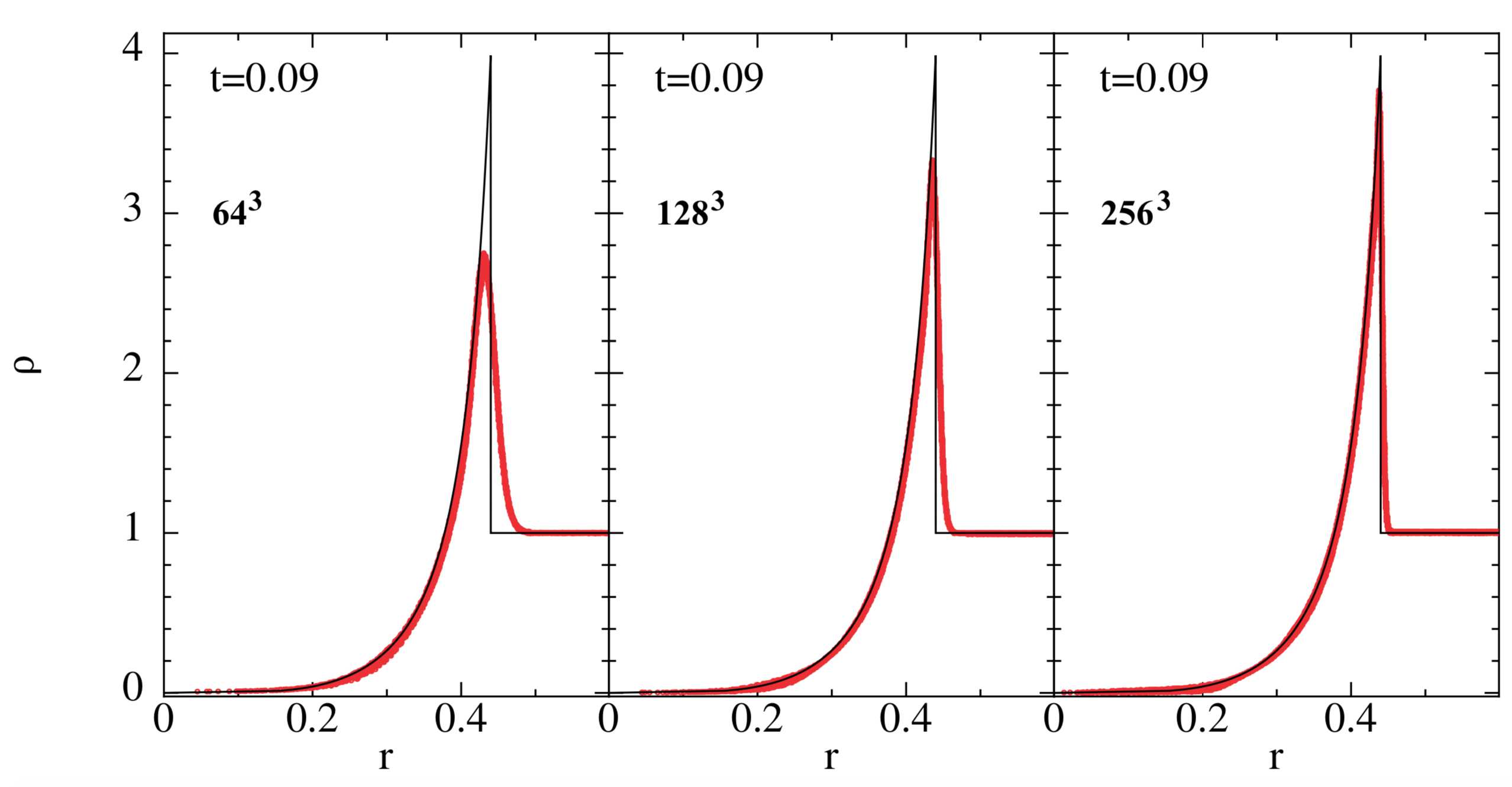
Comments:
• a Sedov-Taylor explosion is a strong, initially point-like explosion into a low-density environment
• the exact solution is known (black line, second plot)
• it is a good numerical test, because many codes (particle- and grid-based) produce
  • (substantial) deviations from spherical symmetry
  • a lot of noise behind the shock front
• the MAGMA2 solution shows no visible deviation from perfect symmetry
• in the second plot *every single particle* is shown (as red dots), i.e. we have an extremely well behaved particle distribution; this is the result of careful initial conditions and the Wendland-kernel + 300 neighbours



2. Kelvin-Helmholtz instability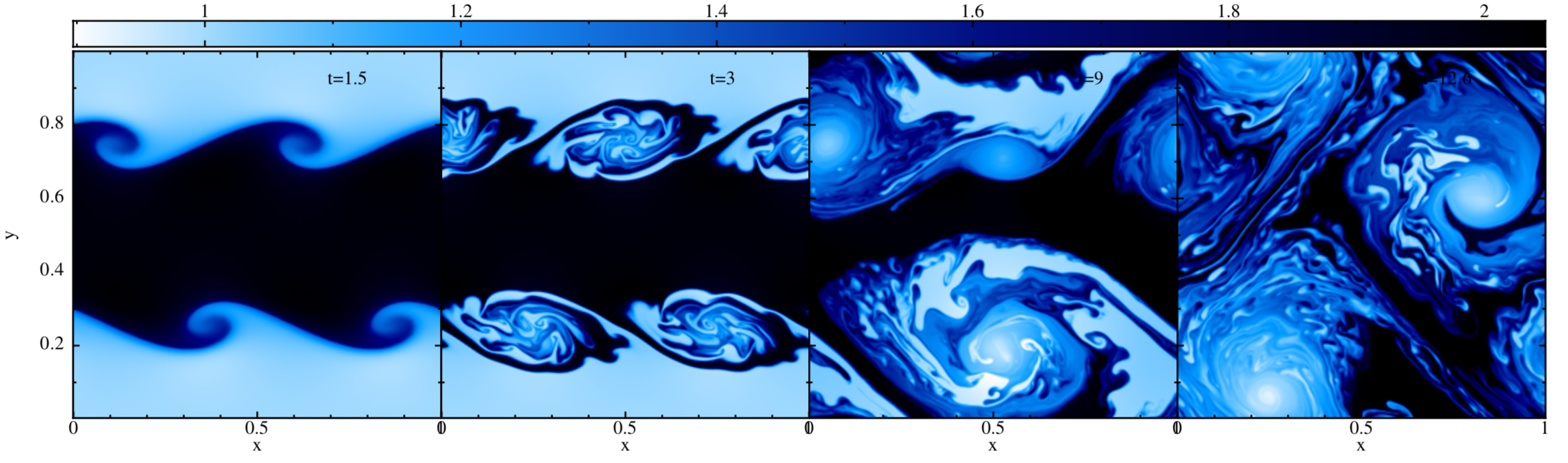



click on the following picture to play the movie (left:density; right: dissipation parameter)
Comments:
• the shown Kelvin Helmholtz test is usually considered challenging for SPH and for "traditional formulations" the instability grows too slowly (if at all), see McNally et al. (2012)
• test is run in "pseudo-2D" (= thin 3D-slice) with the full 3D code
• the MAGMA2 results show an accurate growth of the instability, even at low resolution, see Fig.19 in the MAGMA2 code paper
• the major difference compared with "standard SPH" comes from the slope-limited reconstruction, the second most import effect for this test comes from the more accurate gradients, see Fig. 20 in the code paper
• the movie shows the density on the left and the dissipation parameter, steered by our entropy-method, on the right; for comparison keep in mind that many "traditional SPH" methods use a constant dissipation parameter of ~1



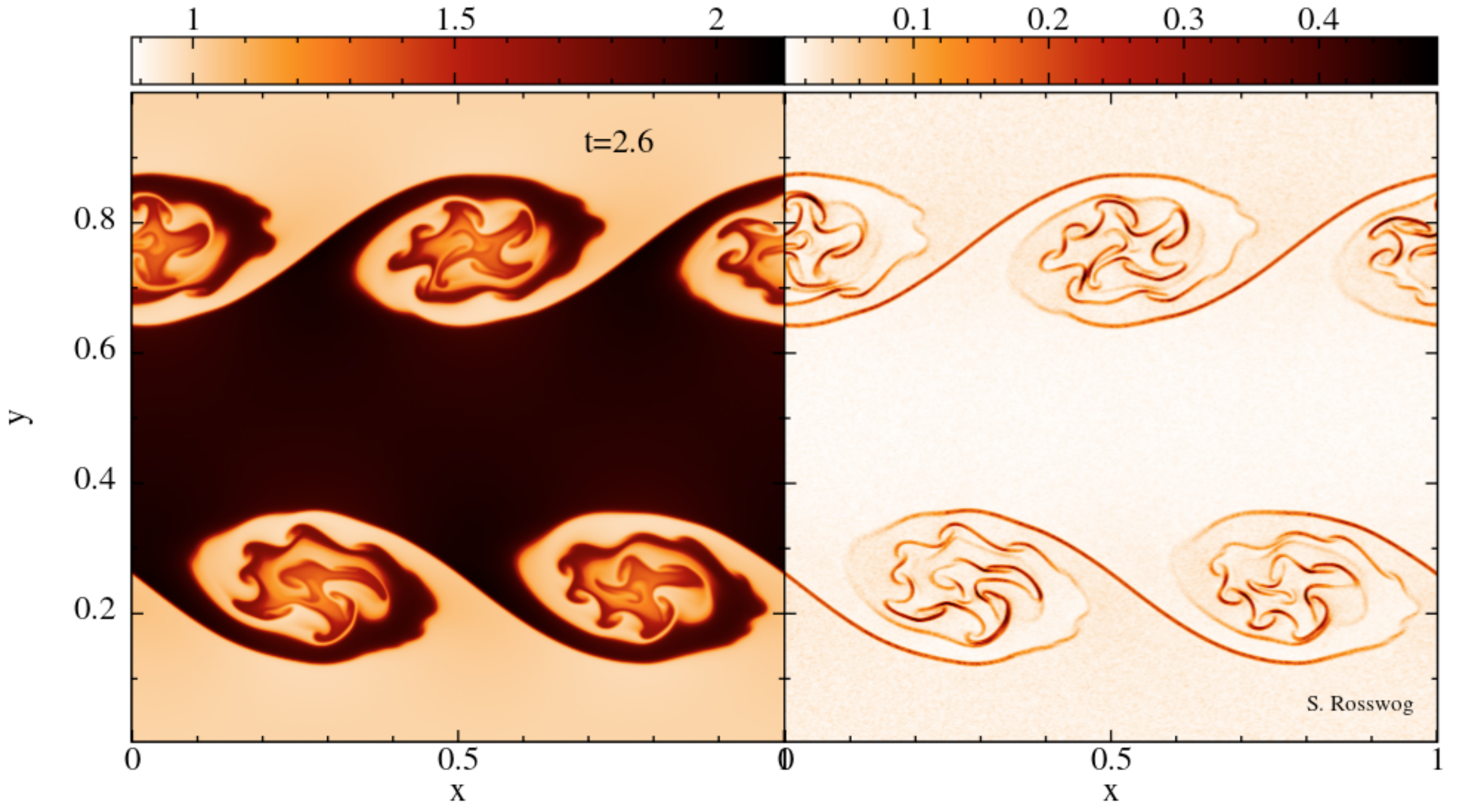
3. Rayleigh-Taylor instability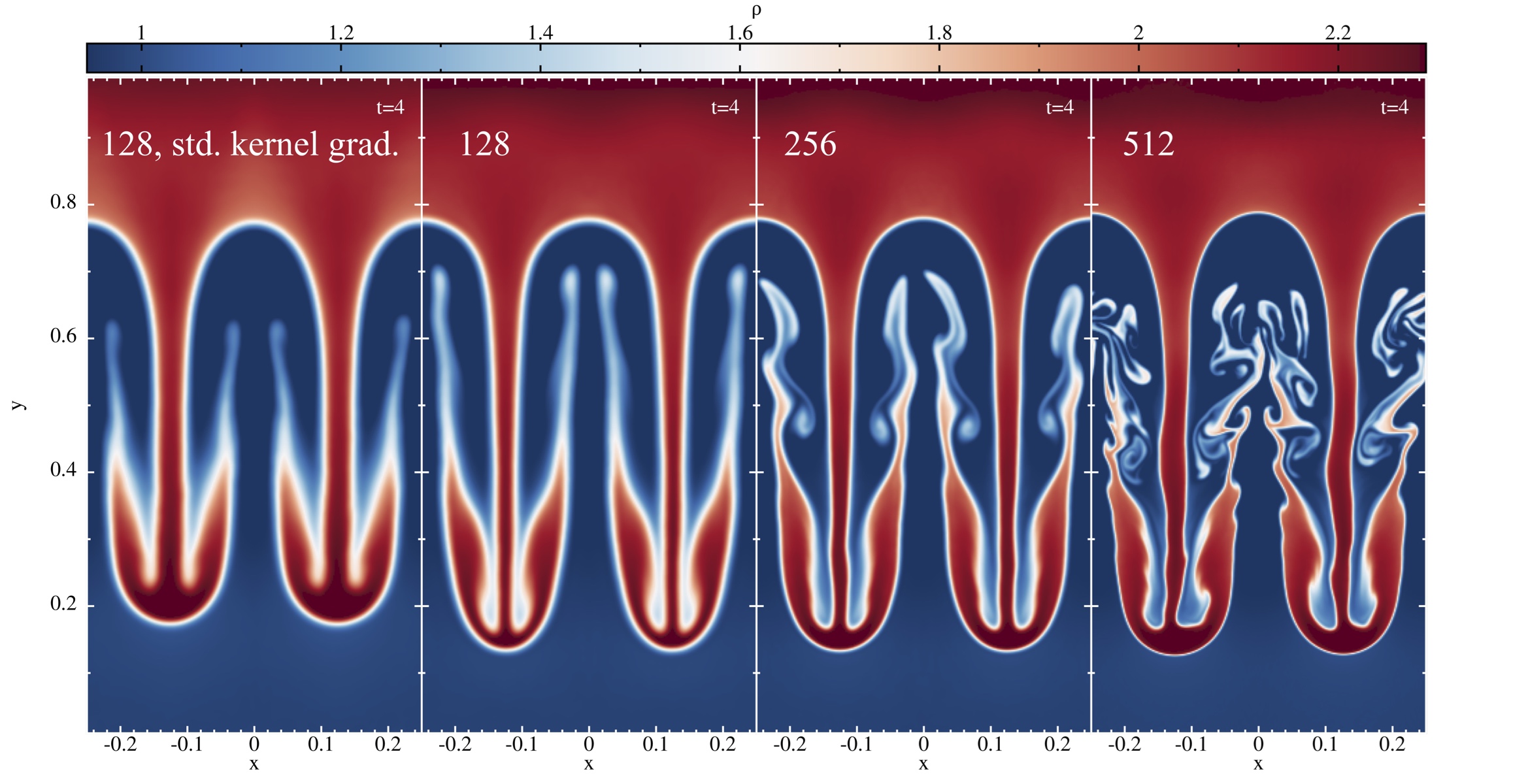



Comments:
• Rayleigh-Taylor instabilities are another standard hydrodynamics test
• test is run in "pseudo-2D" (= thin 3D-slice) with the full 3D code
• the MAGMA2 results agree very well in this test with other state-of-the-art codes



4. Schulz-Rinne tests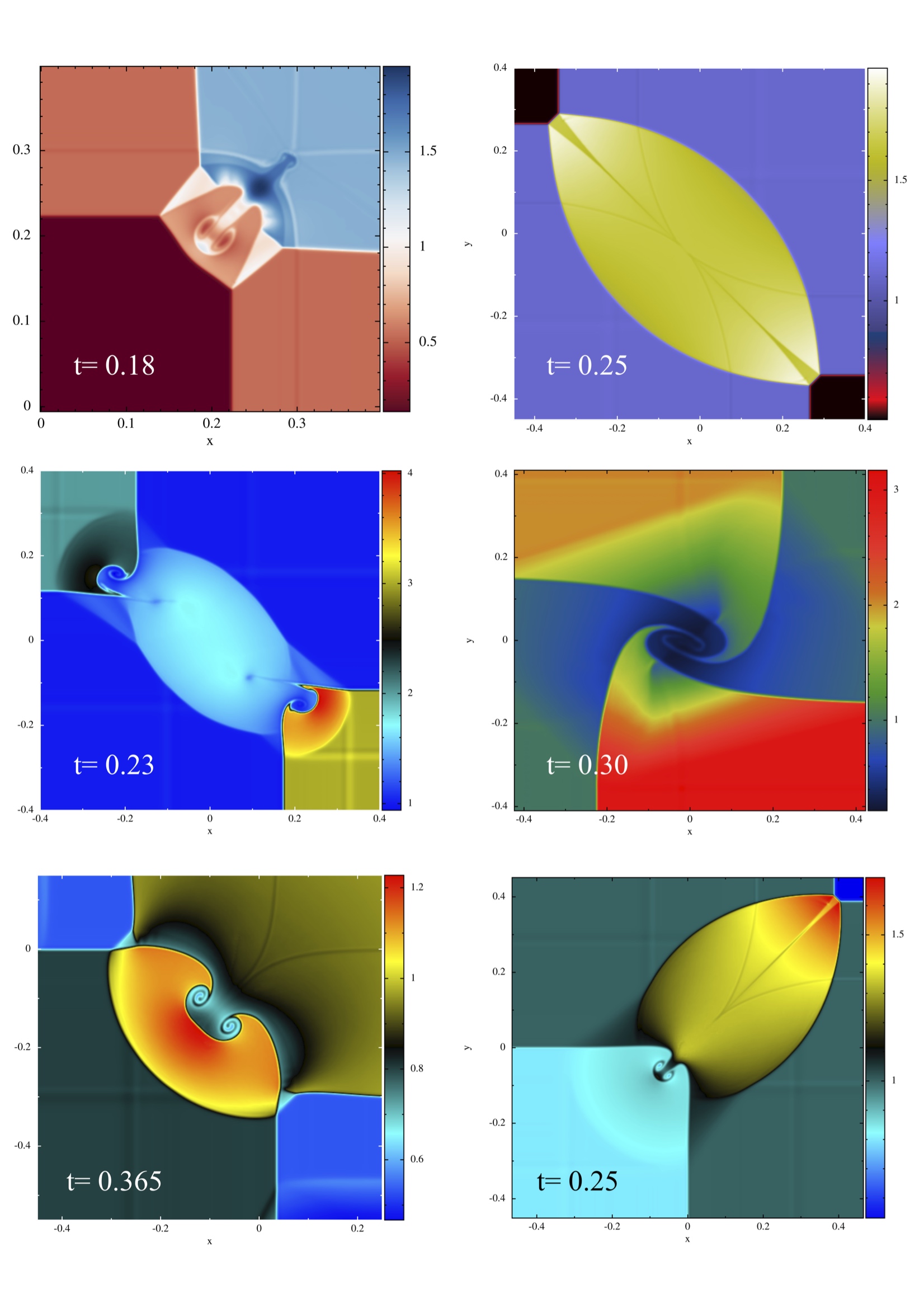


Comments:
• Schulz-Rinne (1993) designed a set of very challenging benchmark tests where complex wave patterns emerge and in particular a combination of shocks and vorticity creation occurs
• no analytic solutions are known for these tests, but many numerical solutions from modern Eulerian codes; actually these tests have hardly ever been tackled with SPH, it seems...
• again, the MAGMA2 results are in very good agreement with those from modern Eulerian codes



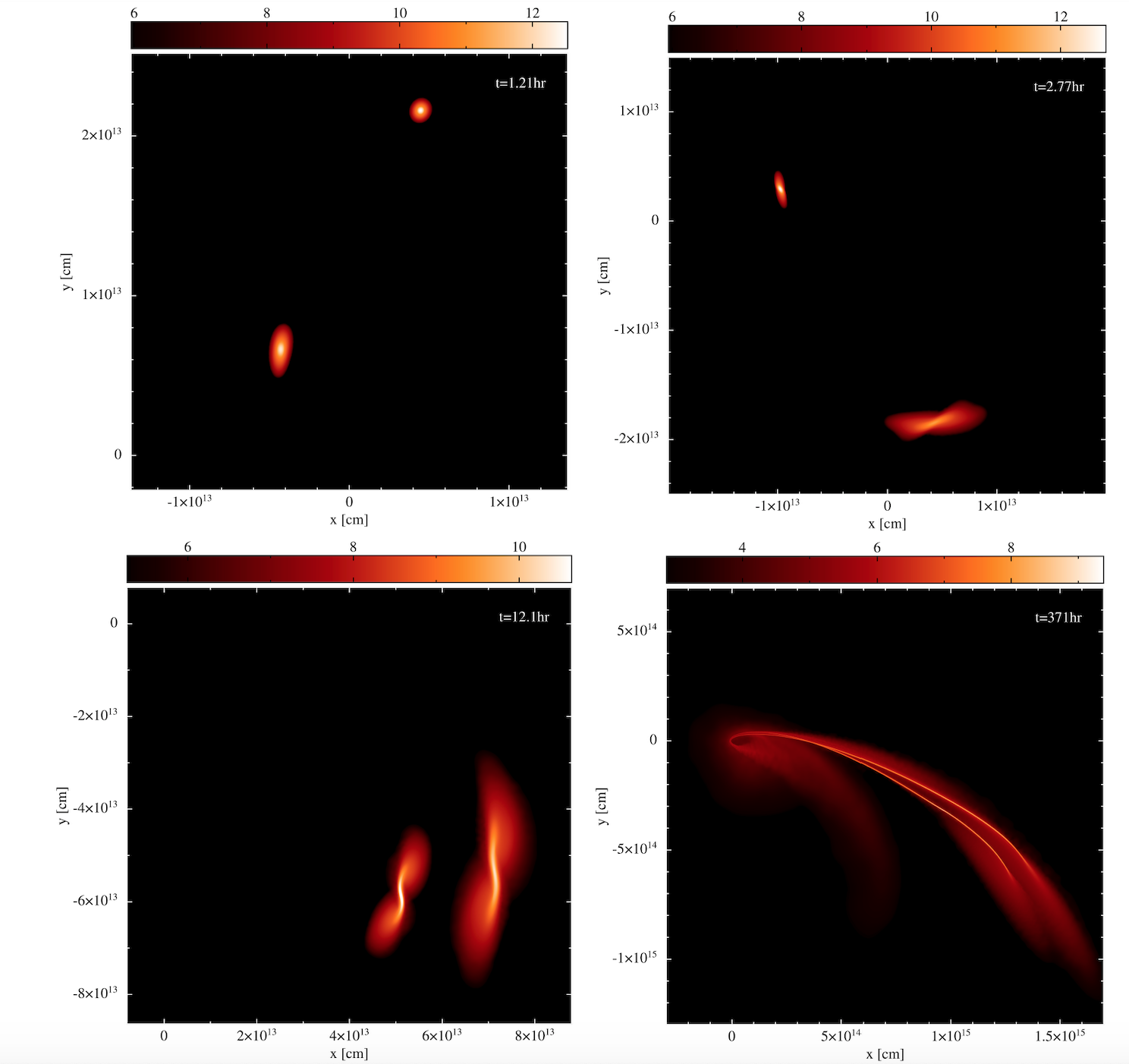
5. Tidal disruptions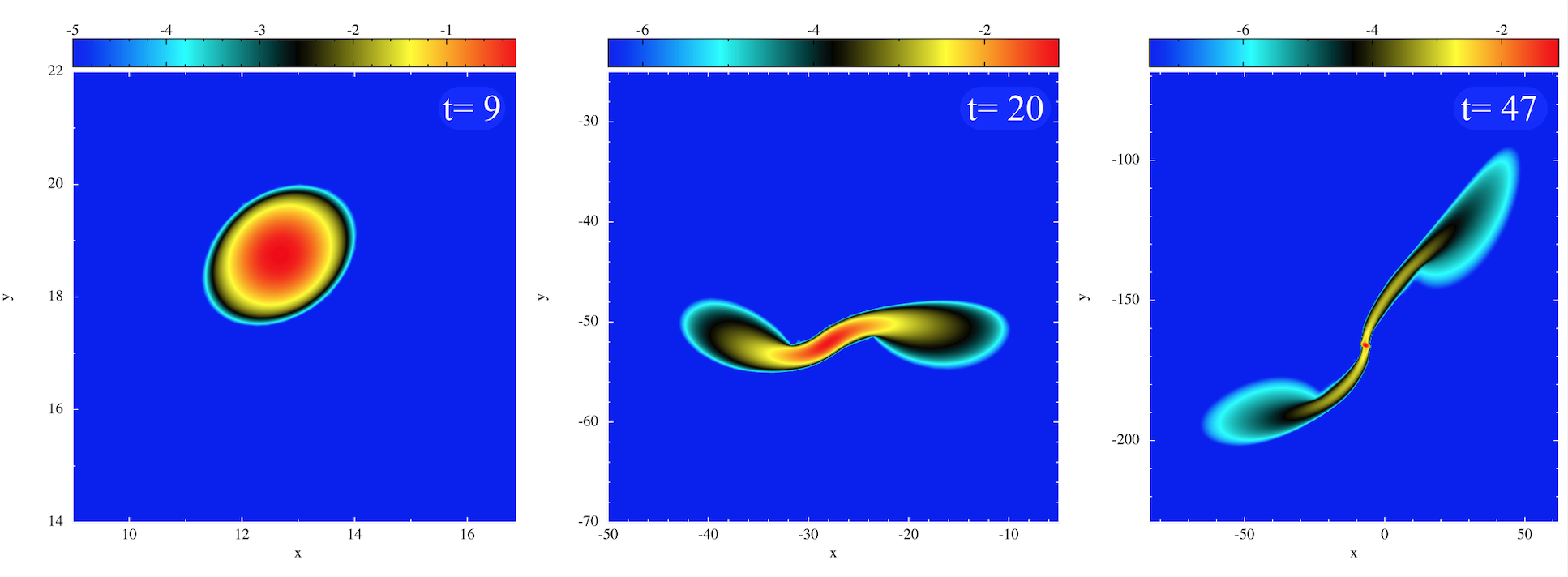

partial disruption of 0.5 solar mass white dwarf by a 1000 solar mass black hole:

"double disruption" of a stellar binary by a supermassive black hole of 1 million solar masses:

Comments:
• Tidal Disruption Events (TDEs) pose serious computational challenges:
  • the disrupted star is often "spagettified" and much larger than the orignal stars
  • often self-gravity is important for structure of the debris and for weak encounters often leads to the re-formation of a central core in the centre of the "spagetti", see panel 3 in the first TDE plot
  • the geometry of the double-disruption remnant, in particular its self-gravity, poses a major challenge for most hydrodynamics methods